1과목: 과목 구분 없음
1. 수열 {an}의 첫째항부터 제n항까지의 합을 Sn이라 하자. Sn = 2n2-n일 때, a10의 값은?
- 34
- 35
- 36
- 37
2. 좌표평면 위의 점(4, 2)를 지나고 직선 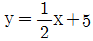 와 수직인 직선의 방정식은?
와 수직인 직선의 방정식은?

- y = -2x + 10
- y = 2x - 6
- y = -2x
3. 서로 독립인 두 사건 A, B에 대하여 P(B) = 1/2, P(A∪B) = 5/8 일 때, P(A)의 값은?
- 1/8
- 1/4
- 3/8
- 1/2
4. 다음 함수 f(x)가 x=1에서 미분가능할 때, f(2)의 값은?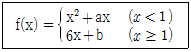
- 9
- 11
- 13
- 15
5. x=2+√3, y=2-√3 일 때, 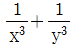 의 값은?
의 값은?
- 50
- 51
- 52
- 53
6. 집합 A={-1, 0, 1}에 대하여 A에서 A로의 함수 f(x)중 항등함수인 것은?
- f(x) = -x
- f(x) = x2
- f(x) = x3
- f(x) = |x|
7.  의 값은?
의 값은?
- 36
- 48
- 54
- 60
8. 다음 함수 f(x)가 모든 실수 x에 대하여 연속일 때, a+4b의 값은? (단, a, b는 상수이다)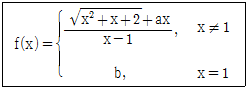
- -6
- -7
- -8
- -9
9. 함수 f(x)에 대하여 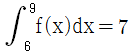 ,
, 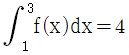 ,
, 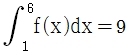 일 때, 정적분
일 때, 정적분  의 값은?
의 값은?
- 6
- 8
- 10
- 12
10. 좌표평면 위의 두 집합 A와 B의 교집합 A∩B가 나타내는 영역의 넓이는?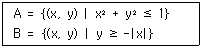
- π/4
- π/2
- 3π/4
- π
11. 계수가 실수인 이차방정식 x2-4x+a-7=0 이 실근을 가질 때, 이차방정식 x2+2x+3a-5=0 이 허근을 갖도록 하는 정수 a의 개수는?
- 6
- 7
- 8
- 9
12. 1, 2, 3, 4, 5, 6, 7의 일곱 개의 숫자 중 서로 다른 세 개의 숫자를 사용하여 만들 수 있는 세 자리의 자연수의 개수는?
- 120
- 180
- 210
- 240
13. 0이 아닌 실수 k에 대하여 함수  의 그래프를 x축의 방향으로 4만큼, y축의 방향으로 2만큼 평행이동한 그래프가 점(2, 4)를 지날 때, k의 값은?
의 그래프를 x축의 방향으로 4만큼, y축의 방향으로 2만큼 평행이동한 그래프가 점(2, 4)를 지날 때, k의 값은?
- -2
- -1
- 1
- 2
14. 두 양의 실수 x, y에 대하여 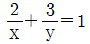 일 때, x+y의 최솟값은?
일 때, x+y의 최솟값은?
- 6-2√5
- 6+2√5
- 5-2√6
- 5+2√6
15. 수열 {an}에 대하여 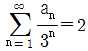 일 때,
일 때, 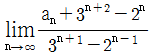 의 값은?
의 값은?
- 3
- 10/3
- 11/3
- 4
16. y=mx의 그래프가 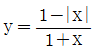 의 그래프와 세 점에서 만나도록 하는 m의 범위가 a < m < b 일 때, a+b의 값은?
의 그래프와 세 점에서 만나도록 하는 m의 범위가 a < m < b 일 때, a+b의 값은?
- -3-√2
- -3+√2
- -3-2√2
- -3+2√2
17. 등식 x3+x2+x+1=a(x+1)3+b(x+1)2+c(x+1)+d 가 x에 대한 항등식일 때, 상수 a, b, c, d에 대하여 a+b+c+d 의 값은?
- 1
- 3
- 5
- 7
18. 10a = 16, 5b = 256 일 때,  의 값은?
의 값은?
- log105
- log52
- 1
- 2
19. 집합 A = {x | 2019 ≤ 2x +9 ≤ 2219,  는 정수}의 원소의 개수는?
는 정수}의 원소의 개수는?
- 20
- 21
- 22
- 23
20. 다항식 x10-2x+4를 (x-1)2로 나누었을 때의 나머지는?
- 5x + 8
- 5x - 8
- 8x + 5
- 8x – 5







따라서, 지나는 점 (4, 2)와 기울기가 2인 직선의 방정식을 구하면 됩니다.
기울기가 2이므로, 일반적인 기울기-절편 형태의 방정식인 y = 2x + b 에서 b를 구하기 위해 (4, 2)를 대입합니다.
2 = 2(4) + b
b = -6
따라서, 구하고자 하는 직선의 방정식은 y = 2x - 6 이 됩니다.
하지만, 보기에서는 y = -2x + 10 이 정답으로 주어졌습니다. 이는 기울기가 -1/2인 직선과 수직이므로, 기울기가 2인 직선의 방정식은 y = -2x + 10이 됩니다.
따라서, 정답은 y = -2x + 10 입니다.