1과목: 과목 구분 없음
1. 다음 그림과 같이 4개의 볼트(a, b, c, d)로 체결된 브라켓 (bracket)이 편심하중 P를 받고 있을 때 각 볼트가 받는 전단응력의 관계로 옳은 것은?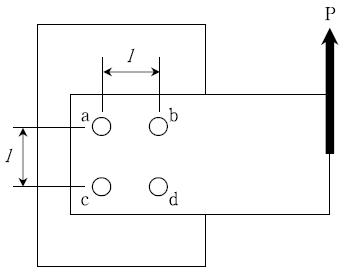
- a와 b의 전단응력의 크기가 같다.
- b와 c의 전단응력의 크기가 같다.
- c와 d의 전단응력의 크기가 같다.
- b와 d의 전단응력의 크기가 같다.
2. 토크 T를 받고 있는 성크키(sunk key)에 생기는 전단응력을 τ, 압축응력을 σc라 할 때 키의 높이 h와 폭 b의 관계로 옳은 것은? (단, τ/σc=1/3 이다)
- h=b
- h=2/3b
- h=b/2
- h=b/3
3. 웜기어 장치에서 웜의 리드각(γ)에 대한 식으로 옳은 것은?
4. 클러치(clutch)에 대한 설명으로 옳지 않은 것은?
- 축방향의 추력이 동일할 때 원판클러치는 원추클러치보다 더 큰 마찰력을 발생시킬 수 있다.
- 전자클러치는 전류의 가감에 의하여 접촉 마찰력의 크기를 조절할 수 있다.
- 삼각형 맞물림 클러치는 사각형 맞물림 클러치에 비해 작은 하중의 전달에 적합하다.
- 축방향 하중이 같을 경우 다판 클러치와 단판 클러치의 전달 토크는 동일하다.
5. 원통마찰차에서 회전속도가 NA이고 직경이 DA인 원동차가 회전 속도 NB이고 직경이 DB인 종동차와 외접하고 있을 때 중심 거리는?
6. 다음 그림과 같이 접착제를 사용하여 벨트를 잇고자 한다. 접착제의 전단강도가 인장강도보다 73.2% 더 크다고 할 때 접착면의 최적 경사각은? (단, √3=1.732이다)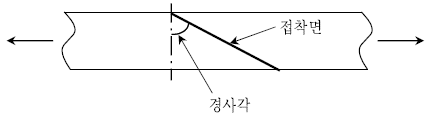
- 0 °
- 30 °
- 45 °
- 60 °
7. 피로한도 280MPa, 항복강도 450MPa, 극한강도가 560MPa인 재료의 굿맨선(Goodman line)을 나타내는 식은? (단, σa는 응력진폭, σm은 평균응력으로 단위는 MPa이다)
8. 바깥지름이 50mm이고 골지름이 44mm인 한줄 사각나사를 2.5회전시키면 25mm 전진한다고 한다. 나사의 리드각을 α라고 할 때 tanα의 값은?
- 0.034
- 0.051
- 0.068
- 0.082
9. 두께가 3mm인 두 판재를 한줄 겹치기로 리벳이음 할 때 리벳의 지름이 6 mm라면 필요한 피치[mm]는? (단, 리벳의 전단강도는 판재의 인장강도의 0.5배이고, π=3.14이다)
- 16.71
- 10.71
- 18.00
- 12.00
10. 바하(Bach)의 축공식에 대한 설명으로 옳은 것은? (단, N은 회전수 (rpm), Hps는 전달 마력(PS)이다)
- 축의 강도설계에서 축길이 1 m에 대하여 비틀림각이 0.25 ° 이내가 되는 조건에서 축지름을 구한다.
- 축의 강성설계에서 축길이 1 m에 대하여 비틀림각이 0.25 ° 이내가 되는 조건에서 축지름을 구한다.
- 축지름
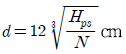 이다.
이다. - 축지름
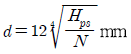 이다.
이다.
11. 체인 전동의 특성에 대한 설명으로 옳지 않은 것은?
- 체인의 탄성으로 어느 정도 충격하중을 흡수할 수 있다.
- 초기장력이 필요없어 정지 시 장력이 작용하지 않는다.
- 체인의 길이 조절과 다축 전동이 쉽다.
- 미끄럼이 있어 일정한 속도비를 얻기 어렵다.
12. 중실(solid) 토션 바에서 토크가 일정할 때 지름과 길이가 각각 2배가 된다면 비틀림 스프링 상수는 몇 배가 되는가?
- 2
- 4
- 8
- 16
13. 한줄 리벳 이음에서 리벳 구멍 사이의 강판이 절단되었다면 한 피치 구간에서 판에 작용한 인장하중 W는? (단, d는 리벳 구멍, p는 피치, t는 강판의 두께, σt는 인장응력이다)
- W=2(p-d)t σt
- W=(p+d)t σt
- W=(p-d)t σt
- W=2(p+d)t σt
14. 스프링에 대한 설명으로 옳지 않은 것은?
- 접시 스프링은 선형 스프링이다.
- 스프링 지수는 소선의 지름에 대한 코일 유효 지름의 비이다.
- 압축 코일 스프링의 주된 응력은 전단응력이다.
- 비틀림 코일 스프링의 주된 응력은 굽힘응력이다.
15. 주물의 기공 결함을 줄이기 위한 대책으로 옳지 않은 것은?
- 용탕의 주입 온도를 최대한 높인다.
- 송탕구(feeder)를 붙여 용탕에 압력을 준다.
- 주형의 통기성을 향상시킨다.
- 주형 내의 수분을 제거한다.
16. 중앙에 집중하중을 받는 단순 지지보의 처짐에 대한 설명으로 옳지 않은 것은?
- 하중의 크기에 비례한다.
- 영 계수에 반비례한다.
- 단면 2차 모멘트에 비례한다.
- 보의 길이의 3제곱에 비례한다.
17. 레이디얼(radial) 하중 P를 받고 있는 볼 베어링의 수명을 20% 연장하고자 할 때 해당 하중의 크기는?
18. 스퍼기어의 치수를 측정하였더니 바깥지름은 대략 250 mm, 이끝원의 원주피치는 약 15.7 mm였다. 보통이라 가정할 때 이 기어의 추정 잇수(Z)와 모듈(m)은? (단, π=3.14이다) (순서대로 Z, m)
- 46, 5
- 46, 6
- 50, 5
- 50, 6
19. 외접하는 원추 마찰차에서 축각이 75 °, 원동차의 원추각이 30 ° 이고 1000rpm으로 회전한다고 할 때 종동차의 회전속도[rpm]는?
- 1000/√2
- 1000√2
- 500
- 2000
20. 전동효율이 0.98인 한 쌍의 스퍼기어에서 구동기어의 피치원 지름이 180mm, 피동기어의 피치원 지름이 90mm일 때 구동기어의 회전토크(T1)에 대한 피동기어의 회전토크(T2)의 비(T2/T1)는?






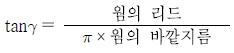
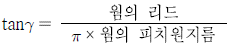
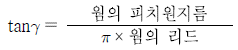
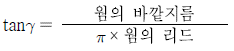
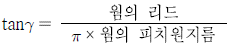 "입니다.
"입니다.
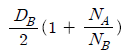

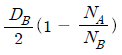
 " 이 정답입니다.
" 이 정답입니다.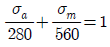
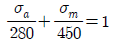
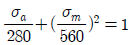
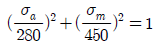
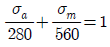
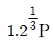
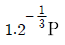
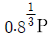

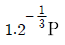 " 입니다.
" 입니다.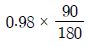

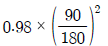
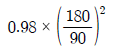
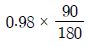 " 이다.
" 이다.
편심하중 P가 작용하면 브라켓은 회전하게 되고, 이로 인해 a와 c 볼트에는 수직방향의 하중이 작용하게 된다. 이에 따라 a와 c 볼트에는 전단응력이 발생하게 되는데, 이는 b와 d 볼트에도 전달된다. 따라서 b와 d 볼트에는 a와 c 볼트에서 발생한 전단응력과 P로 인한 전단응력이 합쳐져서 작용하게 된다. 이때, b와 d 볼트는 동일한 거리에 위치하고 있으므로, a와 c 볼트에서 발생한 전단응력이 동일하게 b와 d 볼트에 전달되어 전단응력의 크기가 같아진다.