1. 기계재료의 표준인장시험에서 얻어지는 진변형률(εT)을 공칭응력 (σ)과 진응력(σT)으로 나타낸 것으로 옳은 것은?
2. 모듈이 4 mm, 중심거리가 150 mm인 외접 스퍼기어에서 회전 각속도비가 0.5일 때, 구동기어의 잇수 Z1과 피동기어의 잇수 Z2를 곱한 값은?
- 800
- 1,250
- 1,700
- 2,150
3. 허용 인장응력이 100 N/mm2, 두께가 10mm인 강판을 용접길이 150mm, 용접효율을 80%로 맞대기 이음을 하고자 한다. 용접부의 허용응력이 80 N/mm2일 때, 목두께[mm]는?
- 10
- 12
- 15
- 16
4. 마찰계수가 극히 작고 마멸이 적기 때문에 NC 공작기계의 이송나사, 자동차의 조향장치, 항공기 날개의 플랩 작동장치에 사용 하는 나사는?
- 사각나사
- 사다리꼴나사
- 볼나사
- 둥근나사
5. 묻힘 키(sunk key)와 축에 동일 토크가 부가되고, 축과 키의 재료가 같다. 축 지름이 20mm, 묻힘 키의 길이가 50mm일 때, 필요한 키의 최소 폭[mm]은?
- 1
- 2
- 3
- 4
6. 기어 이의 간섭이 발생하지 않도록 하기 위한 방법으로 옳지 않은 것은?
- 기어와 피니언의 잇수비를 크게 한다.
- 피니언의 잇수를 최소치수 이상으로 한다.
- 기어의 잇수를 한계치수 이하로 한다.
- 압력각을 크게 한다.
7. 외접하는 두 개의 기어가 맞물려 있고, 중심거리가 150 mm, 하나의 기어 잇수가 80인 두 기어의 모듈이 3일 때, 나머지 기어의 잇수는?
- 20
- 40
- 80
- 120
8. 볼 베어링에 걸리는 하중이 500N, 베어링의 동정격하중이 1,500 N 일 때, 베어링을 10,000시간 이상 사용하기 위한 최대 회전수 [rpm]는?
- 30
- 45
- 300
- 450
9. 마찰면의 바깥지름이 300mm, 안지름이 220mm인 단판클러치에서 축방향으로 밀어붙이는 힘이 1 kN, 마찰계수가 0.3일 때, 전달할 수 있는 토크[Nm]는? (단, 균일한 마모상태로 가정한다)
- 24
- 39
- 78
- 96
10. 평기어를 설계할 때, 언더컷을 방지하기 위한 최소잇수는 압력각에 따라 다르다. 표준치를 갖는 피니언과 맞물리는 기어가 랙일 때, 압력각(p)에 따른 피니언의 이론적 최소잇수(N)는? (단, sin 20°＝0.34, cos 20°＝0.94, tan 20°＝0.36, sin 25°＝0.42, cos 25°＝0.91, tan 25°＝0.47이다)
- p＝20°일 때 N＝18 , p＝25°일 때 N＝12
- p＝20°일 때 N＝12 , p＝25°일 때 N＝18
- p＝20°일 때 N＝18 , p＝25°일 때 N＝22
- p＝20°일 때 N＝22 , p＝25°일 때 N＝18
11. 키의 높이가 h, 폭이 b, 길이가 l 인 묻힘 키(sunk key)에서 높이와 폭을 같게 하였을 때, 키에 작용하는 힘(P)에 의하여 키에 발생하는 전단응력(τ)과 압축응력(σ)의 비(σ/τ))는?
- 0.25
- 0.50
- 1.00
- 2.00
12. 지름이 20mm, 길이가 7 cm인 시편이 시험 후 지름이 10 mm, 길이가 8 cm가 되었을 때, 단면 수축률은?
- 0.55
- 0.65
- 0.75
- 0.85
13. 2줄 나사의 리드각(α)을 계산하는 공식은? (단, d는 나사의 바깥지름, d1은 나사의 골지름, p는 나사의 피치이다)
15. 밸브에 대한 설명으로 옳지 않은 것은?
- 스톱 밸브(stop valve)는 밸브 디스크가 밸브대에 의하여 밸브시트에 직각방향으로 작동한다.
- 버터플라이 밸브(butterfly valve)는 밸브의 몸통 안에서 밸브대를 축으로 하여 원판 모양의 밸브 디스크가 회전하면서 관을 개폐하여 관로의 열림각도가 변화하여 유량이 조절된다.
- 게이트 밸브(gate valve)는 부분적으로 개폐될 때 유체의 흐름에 와류가 생겨 내부에 먼지가 쌓이기 쉽다.
- 체크 밸브(check valve)는 유체를 두 방향으로 흘러가게 하고, 역류를 방지할 목적으로는 적합하지 않다.
16. 주철제 원통형 압력용기의 설계에서 원통의 안지름이 16 mm, 내압이 5MPa, 안전율이 2, 허용인장응력이 40MPa일 때, 용기의 두께[mm]는? (단, 이음매가 없는 경우로 효율은 1로 간주하고, 부식 효과는 무시한다)
- 1
- 2
- 3
- 4
17. 축각이 120°인 원추마찰차의 바깥지름 D1이 300 mm일 때 원추각을 δ1, 바깥지름 D2가 150mm일 때 원추각을 δ2라 할 때, 원추 마찰차의 원추각 비(δ1/δ2)는?
- 1/3
- 1/2
- 2
- 3
18. 저속으로 운전되는 벨트의 두께가 2mm, 폭이 20mm인 벨트전동 장치에서 유효장력이 400 N, 풀리의 접촉각과 마찰계수 곱의 지수값 eμθ=3일 때, 최대 인장응력[MPa]은?
- 5
- 10
- 15
- 20
19. 그림과 같이 5 kN의 물체를 지탱하고 있는 유압크레인에서 핀의 허용면압이 25MPa이고 폭경비가 2일 때, 핀의 직경[mm]은?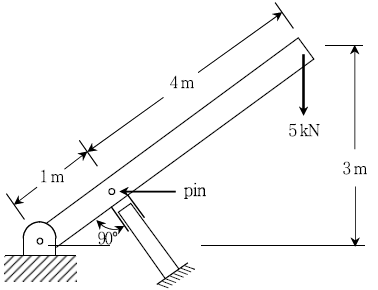
- 20
- 25
- 30
- 40
20. 주로 축간거리가 짧고, 기어전동이 불가능한 경우에 사용되는 체인전동에 대한 설명으로 옳지 않는 것은?
- 전달효율이 크고 슬립이 없는 일정한 속도비를 얻을 수 있다.
- 체인의 탄성으로 어느 정도 충격하중을 흡수할 수 있다.
- 고속회전에 적당하고, 진동 및 소음 발생이 적다.
- 내열, 내유, 내습성이 크며, 유지 및 수리가 쉽다.
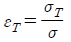
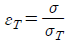
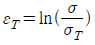
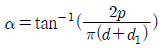
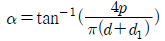
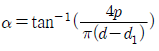
기계재료의 표준인장시험에서 얻어지는 진변형률(εT)은 공칭응력 (σ)과 진응력(σT)으로 나타낼 수 있습니다. 이는 훅의 법칙에 따라 변형률과 응력이 비례하기 때문입니다.
따라서, εT = (σT - σ) / σ 이므로, "
"