1과목: 과목 구분 없음
1. 다음 그림과 같이 a=3 cm, b=5 cm인 직사각형 단면이 있다. x축을 중심으로 1회전 시킬 때 만들어지는 회전체의 체적(cm3)은?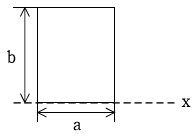
- 60π
- 75π
- 90π
- 150π
2. 다음 그림과 같은 비선형 비탄성 재료로 제작된 봉이 있다. 봉의 길이가 4m이고 단면적이 2cm2일 때, 봉의 길이가 2cm 늘어날 때 까지 하중을 가한 후 모두 제거하였다. 이 봉의 잔류변형률 (residual strain)은? (단, 재료의 특성을 완전 탄소성으로 가정 한다)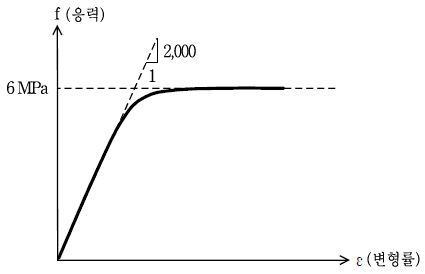
- 0.001
- 0.002
- 0.003
- 0.004
3. 다음 그림과 같이 지점 A는 롤러지점, 지점 B는 고정지점이고 C점에 내부힌지를 배치한 정정보에 하중이 작용하고 있다. B지점의 반력 RB와 MB는? (순서대로 RB, MB)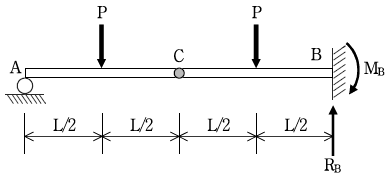
- P, PL/2
- 3P, PL
- 5P/3, 7PL/6
- 7P/4, 5PL/4
4. 다음 그림과 같은 보 구조물 전체가 수평방향으로 이동하지 않고 안정을 유지할 수 있는 수평방향 하중 H[kN]의 최대값은? (단, 힌지부는 마찰계수가 0.2인 바닥면에 놓인 블록에 강결되어 있고, 보의 자중과 롤러부의 마찰은 무시하며 블록의 질량은 11,000 kg, 중력가속도는 10m/sec2이다)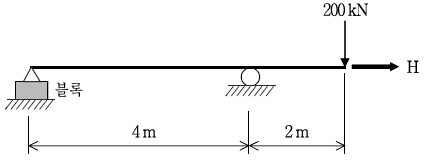
- 44
- 20
- 5
- 2
5. 다음 그림과 같이 집중하중과 등분포하중(작용 길이는 무한대)으로 구성된 하중군이 단순보의 B점에서 A점 방향으로 이동할 때 단순보의 C점에서 발생하는 최대 전단력[kN]은?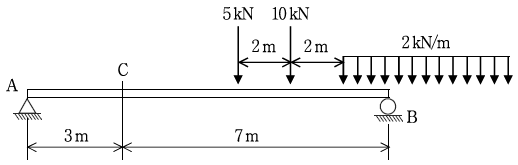
- 9.4
- 9.0
- 9.5
- 3.9
6. 다음 그림과 같이 두 개의 집중하중을 받는 단순보의 내부에서 발생하는 응력을 관찰하기 위하여 A, B, C, D, E점을 선정하였다. 각 점의 응력상태를 기술한 것 중 옳지 않은 것은? (단, A, B, E점은 단면의 상연과 하연에 위치한다)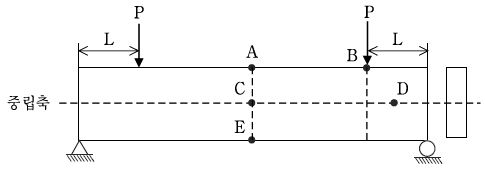
- A점과 B점의 주응력은 같다.
- C점의 주응력은 중립축과 45도 각을 이루는 면에 발생한다.
- D점의 최대 및 최소 주응력은 최대 전단응력과 크기가 같다.
- E점에는 인장 주응력이 발생한다.
7. Euler 탄성좌굴이론의 기본가정 중 옳지 않은 것은?
- 기둥의 재료는 후크의 법칙을 따르며 균질하다.
- 좌굴발생에 따른 처짐(v)은 매우 작으므로 곡률(k)은 d2v/dx2와 같다.
- 좌굴발생 전 양단이 핀으로 지지된 기둥은 초기결함 없이 완전한 직선을 유지하고 어떠한 잔류응력도 없다.
- 좌굴발생 전 중립축에 직각인 평면은 좌굴발생 후 중립축에 직각을 유지하지 않는다.
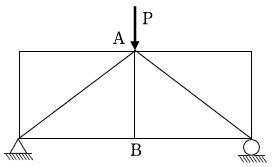
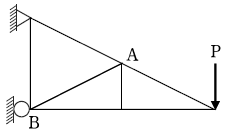
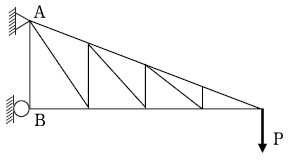
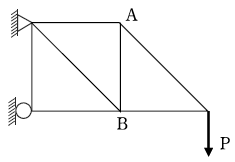
8. 다음 그림과 같이 하중 P가 작용하는 트러스에서 AB부재의 부재력이 0이 아닌 것은?
9. 다음 그림과 같은 정사각형 단주가 있다. 이 단주의 상단 A점에 압축력 10 kN이 작용할 때, 단주의 하단 B점에 발생하는 압축응력[kPa]은?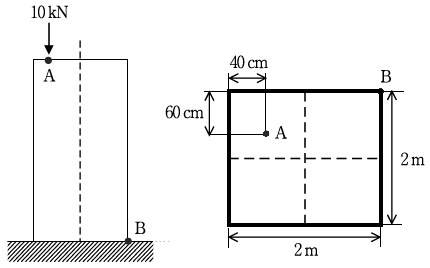
- 1
- 2
- 3
- 4
10. 다음 그림과 같이 단면적을 제외한 조건이 모두 동일한 두 개의 봉에 각각 동일한 하중 P가 작용한다. 봉의 거동을 해석하기 위한 두 개 봉의 물리량 중에서 값이 동일한 것은?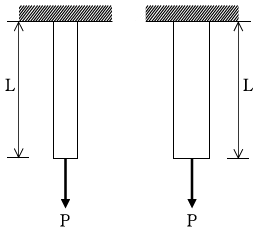
- 신장량
- 변형률
- 응력
- 단면력
11. 길이가 100m이고 한 변의 길이가 1 cm인 정사각형 단면 봉의 온도가 100 °C 하강하여 축방향 변형이 발생되었다. 발생된 변형을 제거하기 위하여 봉에 작용시켜야 하는 축방향 하중은? (단, 봉의 탄성계수 E=200 GPa, 온도선팽창계수 α=1.0 × 10-5/ °C)
- 20 kN(압축)
- 20 kN(인장)
- 200 N(압축)
- 200 N(인장)
12. 다음 그림과 같이 바닥면이 고정되고 전단탄성계수가 G인 고무 받침의 윗면에 전단력 V가 작용할 때 고무받침 윗면의 수평 변위 d 는? (단, 전단력은 고무받침 단면에 균일하게 전달되고 전단변형의 크기는 매우 작다고 가정한다)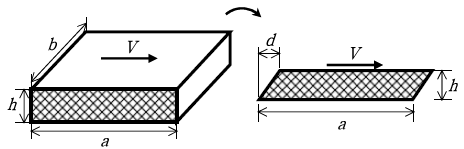
- hV/abG
- GV/abh
- abV/Gh
- V/abhG
13. 다음 그림과 같이 단면적 10m2인 부재에 축방향 인장하중 P가 작용하고 있다. 이 부재의 경사면 ab에 25 Pa의 법선응력을 발생시키는 인장하중 P [N]의 크기를 구하고, 인장하중 P에 의해 부재에 발생하는 최대 전단응력 τmax [Pa]는? (순서대로 P,τmax)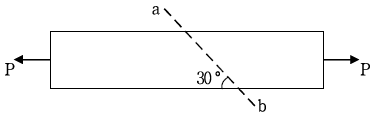
- 1,000, 25√3
- 1,000, 45
- 1,000/3, 60
- 1,000, 50
14. 다음 그림과 같은 구조용 강의 응력-변형률 선도에 대한 설명으로 옳지 않은 것은?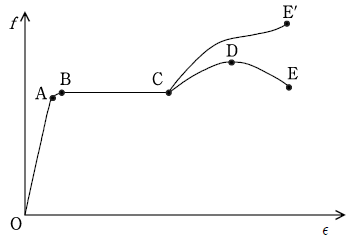
- 직선 OA의 기울기는 탄성계수이며, A점의 응력을 비례한도 (Proportional limit)라고 한다.
- 곡선 OABCE'를 진응력-변형률 곡선(True Stress-Strain Curve)이라 하고 곡선 OABCDE를 공학적 응력-변형률 곡선 (Engineering Stress-Strain Curve)이라 한다.
- 구조용 강의 레질리언스(Resilience)는 재료가 소성구간에서 에너지를 흡수할 수 있는 능력을 나타내는 물리량이며 곡선 OABCDE 아래의 면적으로 표현된다.
- D점은 극한응력으로 구조용 강의 인장강도를 나타낸다.
15. 다음 그림과 같은 구조물을 판별한 것 중 옳은 것은?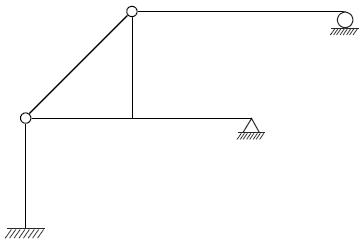
- 정정
- 1차 부정정
- 2차 부정정
- 3차 부정정
16. 다음 그림과 같은 트러스에서 AB부재에 발생하는 부재력 FAB[kN]와 탄성좌굴을 방지하기 위한 AB부재 단면의 최소 단면2차모멘트 I [cm4]는? (단, AB부재 양단의 경계조건은 힌지로 가정하고 탄성계수 E=250 GPa이다) ( 순서대로 FAB, I)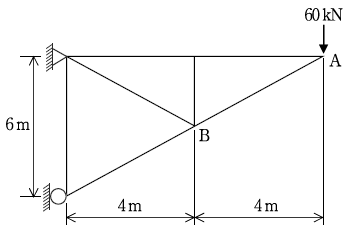
- 100, 250/π2
- 80, 500/π2
- 100, 1,000/π2
- 80, 1,200/π2
17. 다음 그림과 같이 직경 100mm, 길이 10m인 균일단면 원형봉의 B단에 비틀림 모멘트 20 kNㆍ0m가 작용하고 있다. 지점 A에서의 최대 전단응력 τmax[MPa]와 B단의 비틀림각 ø[rad]는? (단, 전단탄성계수 G=80 GPa) (순서대로 τmax, ø)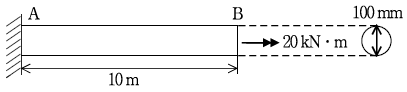
- 200/π, 0.4/π
- 200/π, 0.8/π
- 320/π, 0.4/π
- 320/π, 0.8/π
18. 전 지간에 걸쳐 등분포하중(20 kN/m)이 작용하고 있는 지간 12m인 단순보(사각형 단면의 폭은 100 mm, 높이는 100 mm)가 있다. 지점에서 4m 떨어진 점의 최대 휨응력 f [MPa]와 지간내 발생하는 최대전단응력 τ[MPa]는? (순서대로 f, τ)
- 1,900, 6
- 1,900, 18
- 1,920, 18
- 1,920, 6
19. 다음 그림과 같은 구조물에서 최대 정모멘트가 발생되는 위치는?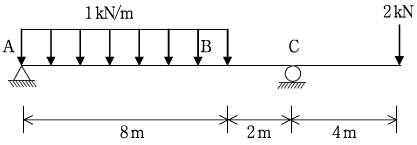
- 점 A에서 3.5m
- 점 A에서 4m
- 점 C
- 점 C에서 5m
20. 다음 그림과 같은 직사각형 탄소성 단면에 대해 기술한 것 중 옳지 않은 것은? (단, h > b이다)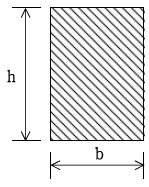
- 도심에 대한 최대 회전반경과 최소 회전반경의 곱은 bh/12이다.
- 단면의 도심과 전단중심은 동일하고, 가로축에 대한 탄성중립축과 소성중립축은 단면 하단에서 h/2에 위치한다.
- 동일 단면으로 장주를 제작하였을 때, 탄성 좌굴축은 단면의 도심을 통과하는 세로축이다.
- 동일 단면으로 지간 중앙에서 집중하중을 받는 길이가 L인 단순보를 제작하였을 때, 소성영역 길이는 2 L/3이다.






원기둥의 체적은 밑면의 넓이(=a*b)와 높이(=2a)를 곱한 후 π를 곱한 것이다.
따라서 원기둥의 체적은 3*5*2*π = 30π 이다.
반구의 체적은 반지름(=b/2)의 세제곱을 2/3한 후 π를 곱한 것이다.
따라서 반구의 체적은 (5/2)^3 * 2/3 * π = 125/3π 이다.
따라서 회전체의 체적은 30π + 125/3π = 75π 이다.
따라서 정답은 "75π"이다.