1과목: 과목 구분 없음
1. 다음 그림과 같은 보에서 반력 RA=3RB의 관계가 성립하는 힘 P1의 크기[kN]는?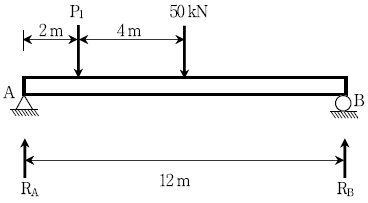
- 150(↓)
- 150(↑)
- 150/7(↓)
- 150/7(↑)
2. 길이가 L인 단면적 A의 인장시험체를 힘 P로 인장하였을 때 δ의 신장이 있었다고 한다. 이 강봉의 전단탄성계수(G)는? (단, 포와 송비는 v이다)
3. 다음 그림과 같은 내민보에서 전단력도가 다음과 같을 때 휨모멘트가 ‘0’이 되는 위치 x [m]는?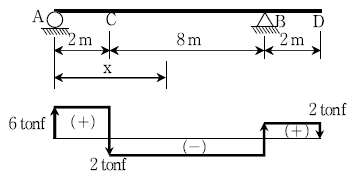
- 2
- 5
- 8
- 10
4. 다음 그림과 같은 게르버보에서 지점 A에서의 휨모멘트[kNㆍm]는? (단, 시계방향을 +로 간주한다)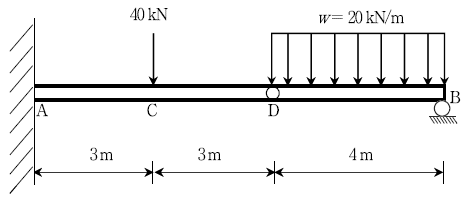
- -120
- 120
- -360
- 360
5. 다음 그림과 같이 수직력이 작용되는 단순보에 부득이하게 작은 구멍을 뚫어야 하는 상황이 발생하였다. 보 구조물에 가장 피해를 h적게 입히는 구멍의 위치는?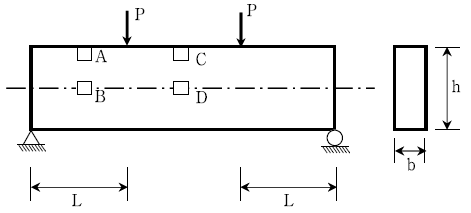
- A
- B
- C
- D
6. 양단힌지 경계조건을 가지는 기둥의 좌굴하중보다 두 배의 좌굴 하중을 가지는 기둥의 경계조건으로 적절한 경우는? (단, 두 경우의 기둥 길이와 단면특성 EI는 같다)
- 1단 힌지, 타단 자유
- 1단 자유, 타단 고정
- 1단 힌지, 타단 고정
- 양단 고정
7. 다음 그림과 같은 트러스 구조물에서 CD부재의 부재력[kN]은?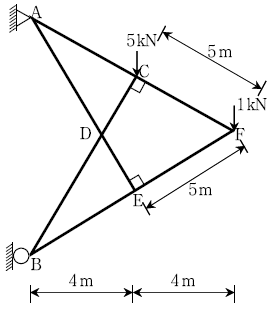
- 4.0 (압축)
- 4.5 (압축)
- 5.0 (압축)
- 5.5 (압축)
8. 다음 그림과 같이 길이 10m이고 높이가 40 cm인 단순보의 상면 온도가 40℃, 하면의 온도가 120℃일 때 지점 A의 처짐각[rad]은? (단, 보의 온도는 높이방향으로 직선변화하며, 선팽창계수 α= 1.2 × 10-5/℃이다)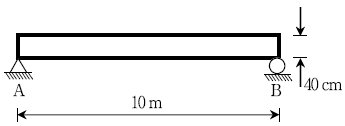
- 0.12
- 0.012
- 0.14
- 0.014
9. 다음 그림과 같은 정정 게르버보에서 최대 휨응력[kPa]은?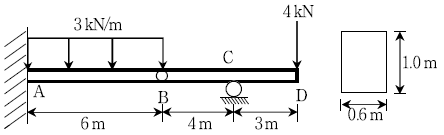
- 15
- 120
- 360
- 720
10. 다음 그림과 같이 무게가 W인 물체가 수평면상에 놓여 있다. 그림과 같이 물체에 수평력 2/3W가 작용할 때 물체의 상태로 옳은 것은? (단, 물체와 수평면 사이의 마찰계수(f)는 0.75이다)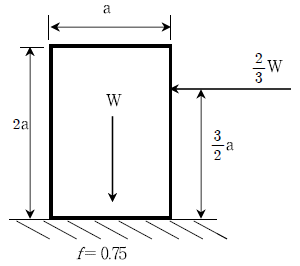
- 수평으로 이동하나 넘어지지는 않는다.
- 수평이동없이 넘어진다.
- 수평이동하며 넘어진다.
- 수평이동도 없고 넘어지지도 않는다.
11. 다음 그림과 같이 수직으로 매달려 있는 균일단면봉이 하중 P1을 받으면 δ1의 변위가 발생하고, P2의 하중을 받으면 δ2의 변위가 발생한다. 하중 P1이 가해진 상태에서 P2의 하중이 작용할 경우이 봉에 저장된 변형에너지 U는? (단, 봉의 자중은 무시하고, 하중 작용시 봉은 선형탄성거동을 한다)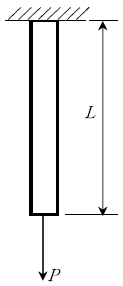
12. 다음 그림과 같은 삼각형 도형의 단면의 성질을 나타낸 것으로 옳지 않은 것은? (단, c는 도심, Q는 단면1차모멘트, I는 단면2차모멘트, Ip는 단면2차극모멘트, 그리고 하첨자는 기준 축을 의미한다)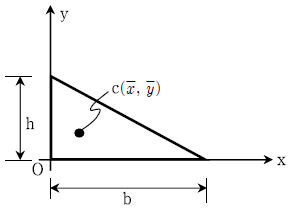
13. 다음 그림과 같이 길이 L인 통나무가 바위 위에 놓여 있다. 통나무의 무게가 1,400 kN일 때, 600 kN의 사람이 왼쪽에서 오른쪽으로 매우 천천히 걷고 있다. 통나무가 수평이 되기 위한 사람의 위치는? (단, 바위와 통나무의 위치는 변하지 않는다)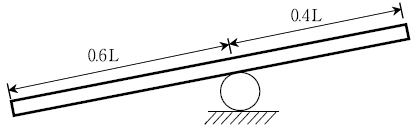
- 왼쪽에서 2L/3
- 왼쪽에서 3L/4
- 왼쪽에서 4L/5
- 왼쪽에서 5L/6
14. 다음 그림과 같이 응력(σ)-변형률(ε) 곡선과 항복강도 270MPa, 탄성계수 180 GPa인 구조용강재로 만들어진 길이 1m의 봉이 축 방향 인장력을 받고 있다. 봉의 신장량이 2.5 mm일 때 인장력을 제거한다면 봉의 잔류 신장량[mm]은?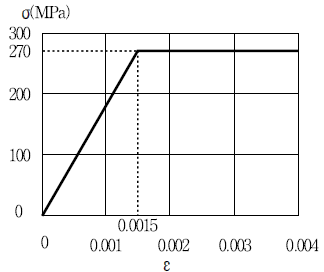
- 0.1
- 0.2
- 0.5
- 1.0
15. 단면적이 5cm2, 길이가 5m인 봉이 온도의 영향으로 탄성변형 1mm 늘어났다. 이 변형을 없애기 위해 작용시켜야할 압축력의 크기[kN]는? (단, 탄성계수는 E=2 × 105MPa이다)
- 10
- 20
- 30
- 40
16. 다음 <그림1>과 같은 트러스 구조물에 수직하중 P가 작용하고 있다. 그리고 모든 트러스 부재에 대한 하중(P)-변위(δ) 곡선은 <그림2>와 같다. 이 구조물이 지지할 수 있는 극한 수직하중 P는? (단, 모든 부재의 탄성계수 E와 단면적 A는 동일하고, 모든 부재는 미소변형 거동을 한다)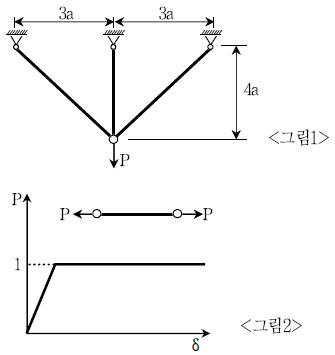
- 13/5
- 3
- 11/5
- 3/5
17. 다음 그림과 같은 강성보(rigid beam)가 A점은 핀(pin)으로, B점과 C점은 스프링상수 k인 스프링으로 지지되어있다. 이 보의 A점의 수직반력은?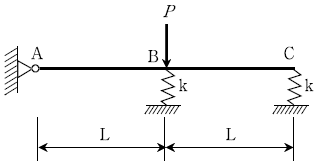
- 0
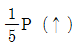
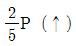
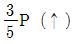
18. 다음 그림과 같은 구조물에서 부재 AB에 발생되는 축력의 크기는?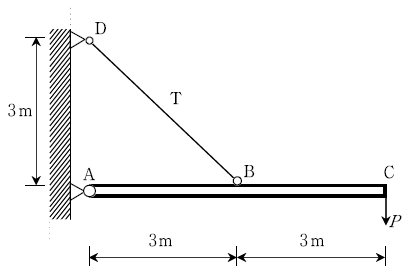
- P/√2
- P
- √2P
- 2P
19. 다음 그림과 같은 보의 경우에 지점 B의 수직반력(RB)은? (단, 길이가 L인 외팔보의 단위하중에 의한 자유단의 처짐은 다음과 같다)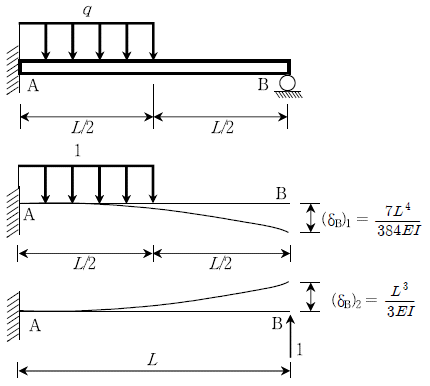
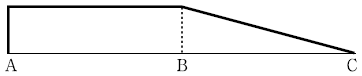
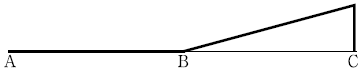
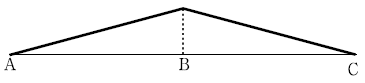
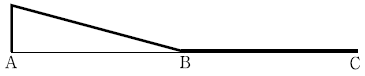
20. 다음 그림과 같은 게르버보에서 지점 A의 반력 모멘트에 대한 정성적인 영향선은?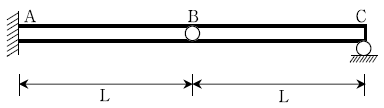






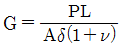
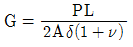
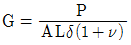
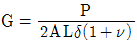
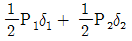
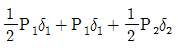
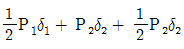
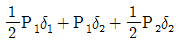
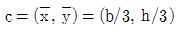
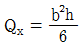
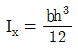
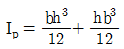
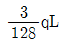
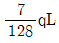
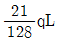
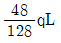
∑Fx=0 에서, P1=RB+RA=4RB 이므로, RA=3RB 이라는 조건을 이용하면 P1=4RB=150(↓) 이 됩니다.
따라서 정답은 "150(↓)" 입니다.