1과목: 과목 구분 없음
1. 다음과 같이 원으로 조합된 빗금친 단면의 도심 C(Centroid)의 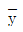 는?
는?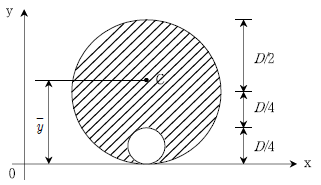
2. 다음과 같이 집중하중이 작용하는 양단 고정보에서 지점의 반력 모멘트가 그림과 같이 A점에 8kNㆍm( )이고 B점에 4kNㆍm (
)이고 B점에 4kNㆍm ( )일 때, C점의 휨모멘트[kNㆍm]는? (단, 자중은 무시한다)
)일 때, C점의 휨모멘트[kNㆍm]는? (단, 자중은 무시한다)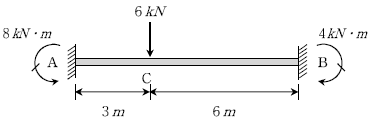
- 16/3
- 20/3
- 22/3
- 25/3
3. 다음과 같은 구조물에서 하중 벡터 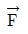 에 의해 O점에 발생되는 모멘트 벡터[kNㆍm]는? (단,
에 의해 O점에 발생되는 모멘트 벡터[kNㆍm]는? (단, 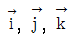 는 각각 x, y, z축의 단위 벡터이다)
는 각각 x, y, z축의 단위 벡터이다)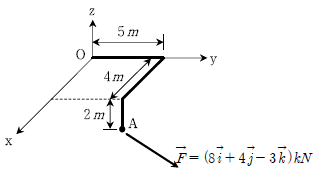
4. 다음과 같이 게르버보에 우측과 같은 이동하중이 지날 때, 지점 B의 반력(RB)의 최대크기[kN]는?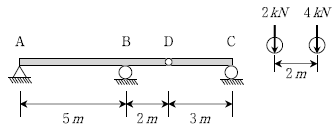
- 24/5
- 26/5
- 36/5
- 38/5
5. 다음과 같이 간접하중을 받고 있는 정정보 AB에 발생되는 최대 연직처짐[m]은? (단, AB 부재의 휨강성 EI=1/48×105kNㆍm2이고, 자중은 무시한다)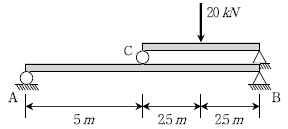
- 0.10
- 0.12
- 0.15
- 0.20
6. 다음과 같이 지름 10mm의 강봉에 3,000kN의 인장력이 작용하여 강봉의 지름이 0.4mm 줄어들었다. 이때 포아송비(Poisson's ratio)는? (단, 강봉의 탄성계수는 2.0 × 105MPa이고, π는 3으로 계산한다)
- 1/3
- 1/4
- 1/5
- 1/6
7. 다음과 같이 게르버보에 하중이 작용하여 발생하는 정모멘트와 부모멘트 중 큰 절댓값[kNㆍm]은? (단, 자중은 무시한다)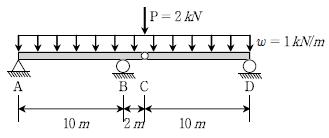
- 12.5
- 13.0
- 13.5
- 16.0
8. 다음 그림(a)와 같은 원형 단면과 그림(b)와 같은 원형관 단면에서 두 단면이 동일한 크기의 전단력을 받을 때, 두 단면에서 발생하는 최대전단응력의 비 (τmax)원형 : (τmax)원형관는?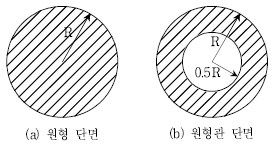
- 8 : 15
- 8 : 13
- 15 : 28
- 15 : 26
9. 다음과 같이 강체가 두 개의 케이블에 지지되어 있다. 강체가 수평을 유지하기 위한 하중 P의 재하위치 x는? (단, 두 케이블의 EA는 같다)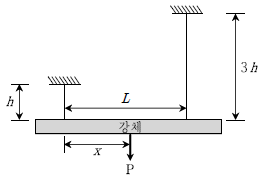
- L/3
- L/4
- 2L/3
- 3L/4
10. 다음과 같이 하중을 받는 보에서 AB 부재에 부재력이 발생되지 않기 위한 CD 부재의 길이 a[m]는? (단, 자중은 무시한다)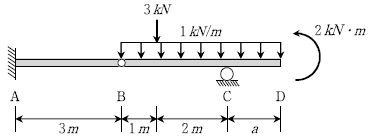
- 2
- 3
- 5
- 6
11. 벽두께 t가 6mm이고, 내반경 r이200mm인 구형압력용기를 제작하였다. 압력 P=6MPa이 구형압력용기에 작용할 경우 막응력의 크기[MPa]는? (단, 구형용기의 벽내부에 발생하는 인장응력 계산 시 내반경 r을 사용하여 계산한다)
- 50
- 100
- 150
- 200
12. 다음과 같이 하중이 작용하는 보 구조물에 발생하는 최대휨모멘트 [kNㆍm]는? (단, 자중은 무시한다)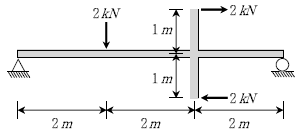
- 2/3
- 4/3
- 5/3
- 8/3
13. 다음과 같은 구조물의 부정정 차수는?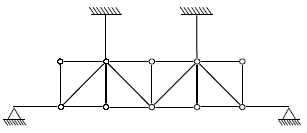
- 2차
- 3차
- 4차
- 5차
14. 가로와 세로의 길이가 4.8mm인 정사각형 단면을 가진 길이가 10 cm인 단순보에 순수 휨모멘트가 작용하고 있다. 단면 최상단에서의 수직변형률(normal strain) ɛx이 0.0012에 도달했을 경우의 곡률 [m-1]의 절댓값은? (단, 부재는 미소변형 거동을 한다)
- 0.1
- 0.2
- 0.5
- 2.0
15. 다음과 같이 구조물에 작용하는 평행한 세 힘에 대한 합력(R)의 O점에서 작용점까지 거리 x[m]는?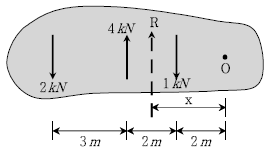
- 0
- 1
- 2
- 3
16. 휨 강성 EI를 갖는 단순보에 다음 그림과 같이 하중이 작용할 때, 지점 A에 발생하는 휨변형에 대한 처짐각 θA는? (단, EI= 1,000kNㆍm2 이고, 자중은 무시한다)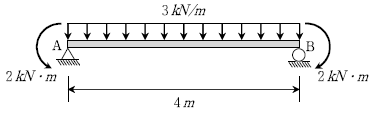
- 0.004(↷)
- 0.004(↶)
- 0.012(↷)
- 0.012(↶)
17. 다음과 같이 수직, 수평의 집중하중을 받고 있는 트러스에서 부재력이 0인 부재의 개수는? (단, 자중은 무시한다)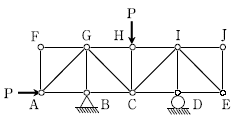
- 6
- 7
- 8
- 9
18. 다음과 같은 강체(Rigid) AD 부재에 축방향으로 하중 P가 작용 하고 있다. 지점 A는 힌지이며, 두 개의 스프링은 B점과 C점에 연결되어 있고, 스프링계수는 동일한 k이다. 강체의 임계좌굴하중 (Pcr)은? (단, 부재는 미소변형 거동을 한다)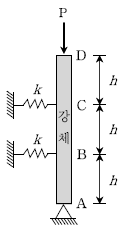
- 4hk/3
- 5hk/3
- 2hk
- 3hk
19. 다음과 같이 길이 L인 단순보와 외팔보에 집중하중 P가 작용하고 있다. 단순보의 B점에 발생되는 수직처짐(δB)과 외팔보 E점에서 발생되는 수직처짐(δE)의 비교값(δE/δB)은? (단, 자중은 무시한다)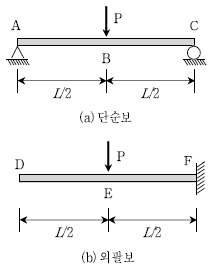
- 0.25
- 0.50
- 2.00
- 4.00
20. 다음과 같이 양단 내민보 전 구간에 등분포하중이 균일하게 작용하고 있다. 이때 휨모멘트도에서 최대정모멘트와 최대부모멘트의 절댓값이 같기 위한 L과 a의 관계는? (단, 자중은 무시한다)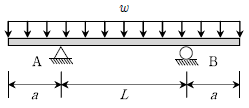





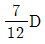
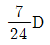
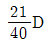
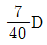

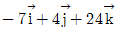
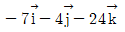
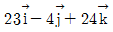
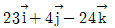
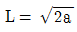
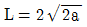
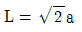
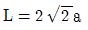
하지만 이 문제에서는 단위가 kNㆍm이 아닌 kNm으로 주어졌기 때문에, 답인 12kNㆍm을 kNm으로 변환해야 한다. 1kNㆍm은 1kNm과 같으므로, 12kNㆍm은 12kNm이 된다.
따라서 정답은 12kNm이다. 이를 기약분수로 나타내면 16/3이 된다.