1과목: 과목 구분 없음
1. 다음 용어들의 짝 중에서 상호 연관성이 없는 것은?
- 전단응력-단면1차모멘트
- 곡률-단면상승모멘트
- 휨응력-단면계수
- 처짐-단면2차모멘트
2. 그림과 같은 구조물의 B지점에서 반력 RB의 값[kN]은? (단, DE는 강성부재이고, 보의 자중은 무시한다)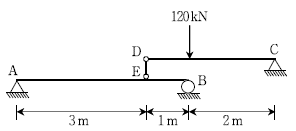
- 120
- 90
- 80
- 60
3. 그림과 같이 받침대 위에 블록이 놓여있다. 이 블록 중심에 F=20 kN이 작용할 때 블록에서 생기는 평균전단응력[N/mm2]은?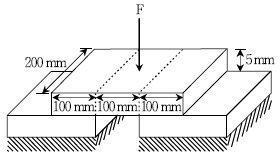
- 1
- 2
- 10
- 20
4. 그림은 단면적 As인 강재(탄성계수 Es)와 단면적 Ac인 콘크리트 (탄성계수 Ec)를 결합한 길이 L인 기둥 단면이다. 연직하중 P가 기둥 중심축과 일치하게 작용할 때 강재의 응력은?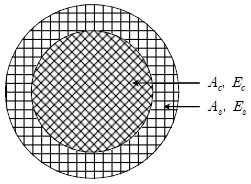
5. 벽면에 수평으로 연결된 와이어가 있다. 중심각이 2θ인 원호 형태로 처짐이 발생된다면 이때 생기는 와이어의 변형률은? (단, θ의 단위는 radian이다)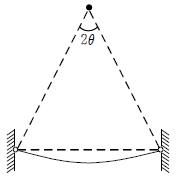
6. 그림에서 캔틸레버보의 B점 처짐이 단순보의 B점 처짐과 같게 되기 위한 단면2차모멘트의 비(Ic/Is)는? (단, 보의 자중은 무시한다)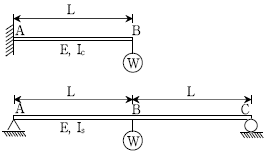
- 1.0
- 1.5
- 2.0
- 2.5
7. 그림과 같은 하중 Q가 작용하는 구조물에서 C점은 마찰연결로 되어 있다. 두 개의 구조물을 분리시키기 위해 필요한 최소 수평력 H는? (단, 구조물의 자중은 무시하고, 정지마찰계수 μ=0.2이다)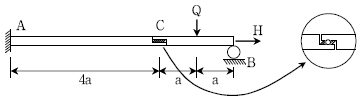
- Q/10
- Q/5
- 3Q/10
- 2Q/5
8. 그림과 같은 포물선 케이블에 수평방향을 따라 전 구간에 걸쳐 연직방향으로 8 N/m의 등분포 하중이 작용하고 있다. 케이블의 최소 인장력의 크기[N]는? (단, 케이블의 자중은 무시하며, 최대 새그량은 2 m이다)
- 2,000
- 3,000
- 4,000
- 5,000
9. 그림과 같은 두 기둥의 탄성좌굴하중의 크기가 같다면, 단면2차 모멘트 I의 비(I2/I1)는? (단, 두 기둥의 탄성계수 E, 기둥의 길이 L은 같다)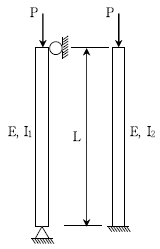
- 1/4
- 1/2
- 2
- 4
10. 그림과 같은 등분포 하중 q를 받는 1차 부정정보의 고정단 모멘트 MA와 반력 RB는? (단, 보의 자중은 무시한다) (순서대로 MA, RB)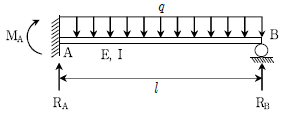
11. 그림과 같은 구조물의 전체 부정정 차수는?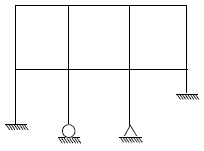
- 15
- 17
- 19
- 21
12. 그림과 같이 하중 50 kN인 차륜이 20 cm 높이의 고정된 장애물을 넘어가는 데 필요한 최소한의 힘 P의 크기[kN]는? (단, 힘 P는 지면과 나란하게 작용하며, 계산값은 소수점 둘째자리에서 반올림한다)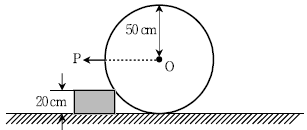
- 33.3
- 37.5
- 66.7
- 75.0
13. 그림과 같이 균일한 직사각형 단면에 전단력 V가 작용하고 있다. a-a 위치에 발생하는 전단응력의 크기를 계산할 때 필요한 단면1차모멘트의 크기는?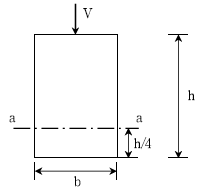
14. 다음 트러스 구조물의 상현재 U와 하현재 L의 부재력[kN]은? (단, 모든 부재의 탄성계수와 단면적은 같고, 자중은 무시한다) (순서대로 U부재력, L부재력)
- 12(압축), 9(인장)
- 12(인장), 6(압축)
- 9(압축), 18(인장)
- 9(인장), 9(압축)
15. 지름이 990 mm인 원통드럼 위로 지름이 10 mm인 강봉이 탄성적으로 휘어져 있을 때 강봉 내에 발생되는 최대 휨응력 [MPa]은? (단, 탄성계수는 2.0 × 105MPa이다)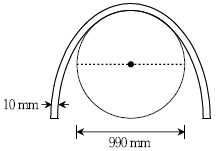
- 495
- 990
- 1,000
- 2,000
16. 그림과 같이 균일 캔틸레버보에 하중이 작용할 때 B점의 처짐각은? (단, 보의 자중은 무시한다)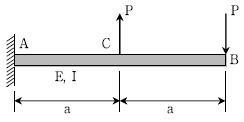
17. 단순보의 전단력선도가 그림과 같을 경우에 CE구간에 작용하는 등분포하중의 크기[kN/m]는?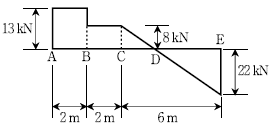
- 3
- 5
- 7
- 14
18. 그림과 같이 하중이 작용하는 보의 B지점에서 수직반력의 크기 [kN]는? (단, 보의 자중은 무시한다)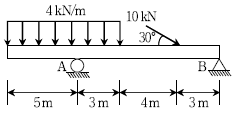
- 0.2
- 0.3
- 3.8
- 6.7
19. 안쪽 반지름(r)이 300mm이고, 두께(t)가 10mm인 얇은 원통형 용기에 내압(q) 1.2MPa이 작용할 때 안쪽 표면에 발생하는 원주방향응력(σy) 또는 축방향응력(σx)으로 옳은 것(단위는 MPa)은? (단, 원통형 용기의 안쪽 표면에 발생하는 인장응력을 구할 때는 안쪽 반지름(r)을 사용한다)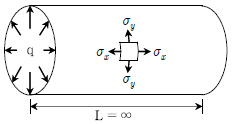
- σy=24
- σy=48
- σx=18
- σx=36
20. 그림 (a)와 같은 단순보 위를 그림 (b)와 같은 이동분포하중이 통과할 때 C점의 최대 휨모멘트[kNㆍm]는? (단, 보의 자중은 무시한다)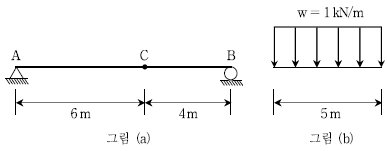
- 8
- 9
- 10
- 11






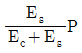


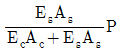

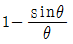
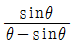
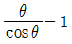
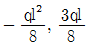
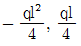
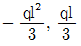
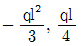
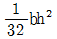
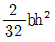
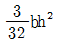
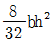
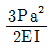
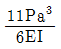
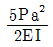
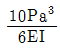
전단응력은 단면1차모멘트와 관련이 있으며, 처짐은 단면2차모멘트와 관련이 있습니다.
곡률은 단면의 곡률을 나타내며, 단면상승모멘트는 단면의 곡률에 따라 발생하는 모멘트를 의미합니다.
하지만 휨응력은 단면계수와 관련이 있지만, 다른 용어들과는 직접적인 연관성이 없습니다.