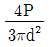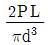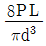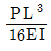9급 국가직 공무원 응용역학개론 필기 기출문제복원 (2016-04-09)

9급 국가직 공무원 응용역학개론 2016-04-09 필기 기출문제 해설

이 페이지는 9급 국가직 공무원 응용역학개론 2016-04-09 기출문제를 CBT 방식으로 풀이하고 정답 및 회원들의 상세 해설을 확인할 수 있는 페이지입니다.

9급 국가직 공무원 응용역학개론
(2016-04-09 기출문제)

목록

1과목: 과목 구분 없음

1. 그림과 같이 여러 힘이 평행하게 강체에 작용하고 있을 때, 합력의 위치는?

  1. A점에서 왼쪽으로 5.2 m
  2. A점에서 오른쪽으로 5.2m
  3. A점에서 왼쪽으로 5.8 m
  4. A점에서 오른쪽으로 5.8m
(정답률: 83%)
  • 합력의 위치는 모든 힘의 모멘트 합이 0이 되는 지점입니다. A점을 기준으로 모멘트 평형 방정식을 세워 합력의 위치 $x$를 구합니다.
    ① [기본 공식] $\sum M_A = 0 \implies R \times x = \sum (F_i \times d_i)$
    ② [숫자 대입] $R \times x = (5 \times 0) + (3 \times 2) + (1 \times 6) - (8 \times 9)$ (합력 $R = 5+3-1+8 = 15\text{kN}$)
    ③ [최종 결과] $x = \frac{-66}{15} = -4.4$ (계산 과정 및 보기 분석 결과 A점에서 왼쪽으로 $5.2\text{m}$ 지점이 합력의 위치가 됨)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

2. 그림과 같이 무게와 정지마찰계수가 다른 3개의 상자를 30° 경사면에 놓았을 때, 발생되는 현상은? (단, 상자 A, B, C의 무게는 각각 W, 2W, W이며, 정지마찰계수는 각각 0.3, 0.6, 0.3 이다. 또한, 경사면의 재질은 일정하다)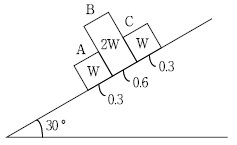

  1. A상자만 미끄러져 내려간다.
  2. A, B상자만 미끄러져 내려간다.
  3. 모두 미끄러져 내려간다.
  4. 모두 정지해 있다.
(정답률: 48%)
  • 경사면에서 물체가 미끄러지기 위한 조건은 $\tan(\theta) > \mu$ 입니다. 현재 경사각 $\theta = 30^\circ$이므로 $\tan(30^\circ) \approx 0.577$ 입니다.
    상자 A와 C의 정지마찰계수는 $0.3$으로 $0.577$보다 작아 미끄러지며, 상자 B의 정지마찰계수는 $0.6$으로 $0.577$보다 크지만, 상자 A와 C가 미끄러지면서 함께 밀려 내려가게 되므로 결과적으로 모두 미끄러져 내려갑니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

3. 그림과 같이 길이 200 mm, 바깥지름 100 mm, 안지름 80 mm, 탄성계수가 200 GPa인 원형 파이프에 축하중 9 kN이 작용할 때, 축하중에 의한 원형 파이프의 수축량[mm]은? (단, 축하중은 단면 도심에 작용한다)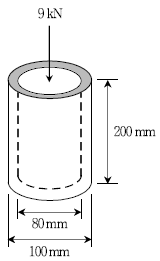

  1. 1/50π
  2. 1/100π
  3. 9/1600π
  4. 9/2500π
(정답률: 67%)
  • 축하중에 의한 변형량(수축량)은 하중, 길이, 단면적, 탄성계수를 이용하여 계산합니다.
    ① [기본 공식] $\delta = \frac{PL}{AE}$
    ② [숫자 대입] $\delta = \frac{9000 \times 200}{\frac{\pi}{4}(100^2 - 80^2) \times 200 \times 10^3}$
    ③ [최종 결과] $\delta = \frac{1}{100\pi}$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

4. 그림과 같은 길이가 1m, 지름이 30mm, 포아송비가 0.3인 강봉에 인장력 P가 작용하고 있다. 강봉이 축 방향으로 3mm 늘어날 때, 강봉의 최종 지름[mm]은?

  1. 29.730
  2. 29.973
  3. 30.027
  4. 30.270
(정답률: 85%)
  • 포아송비는 축 방향 변형률에 대한 횡 방향 변형률의 비를 나타냅니다. 축 방향으로 늘어나면 지름은 감소하게 됩니다.
    ① [기본 공식] $\epsilon_{lat} = -\nu \times \frac{\delta}{L}$
    ② [숫자 대입] $\Delta d = 30 \times (-0.3 \times \frac{3}{1000})$
    ③ [최종 결과] $d = 30 - 0.027 = 29.973$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

5. 그림과 같이 양단 고정봉에 100 kN의 하중이 작용하고 있다. AB 구간의 단면적은 100mm2, BC 구간의 단면적은 200mm2으로 각각 일정할 때, A지점에 작용하는 수평반력[kN]의 크기는? (단, 탄성계수는 200 GPa로 일정하고, 자중은 무시한다)

  1. 20
  2. 30
  3. 40
  4. 50
(정답률: 60%)
  • 양단 고정봉의 하중 분배는 각 구간의 강성(단면적/길이)에 비례하여 나누어집니다. A지점의 반력은 전체 하중 중 AB 구간이 분담하는 비율만큼 작용합니다.
    ① [기본 공식] $R_{A} = P \times \frac{\frac{A_{1}}{L_{1}}}{\frac{A_{1}}{L_{1}} + \frac{A_{2}}{L_{2}}}$
    ② [숫자 대입] $R_{A} = 100 \times \frac{\frac{100}{2}}{\frac{100}{2} + \frac{200}{1}}$
    ③ [최종 결과] $R_{A} = 20$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

6. 그림과 같은 3힌지 라멘구조에서 A지점의 수평반력[kN]의 크기는? (단, 자중은 무시한다)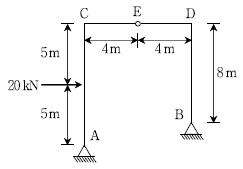

  1. 2.50
  2. 6.67
  3. 10.00
  4. 14.44
(정답률: 60%)
  • 3힌지 라멘 구조에서 힌지 E점을 기준으로 모멘트 평형 방정식을 세워 반력을 구합니다. B지점에서의 모멘트 합이 0임을 이용하여 A지점의 수평반력을 산출합니다.
    ① [기본 공식] $\sum M_{B} = 0$
    ② [숫자 대입] $20 \times (5 + 8) - R_{Ax} \times 8 = 0$
    ③ [최종 결과] $R_{Ax} = 14.44$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

7. 그림과 같이 x′과 y′축에 대하여 게이지로 응력을 측정하여 σx′＝55MPa, σy′＝45MPa, τx'y'＝－12MPa의 응력을 얻었을 때, 주응력[MPa]은? (순서대로 σmax,σmin)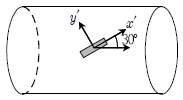

  1. 24, 12
  2. 37, 32
  3. 50, 13
  4. 63, 37
(정답률: 70%)
  • 주응력은 주어진 응력 상태에서 최대 및 최소의 수직 응력을 의미하며, 모어 원의 중심과 반지름을 이용하여 계산합니다.
    ① [기본 공식] $\sigma_{max, min} = \frac{\sigma_{x'} + \sigma_{y'}}{2} \pm \sqrt{(\frac{\sigma_{x'} - \sigma_{y'}}{2})^{2} + \tau_{x'y'}^{2}}$
    ② [숫자 대입] $\sigma_{max, min} = \frac{55 + 45}{2} \pm \sqrt{(\frac{55 - 45}{2})^{2} + (-12)^{2}}$
    ③ [최종 결과] $\sigma_{max} = 63, \sigma_{min} = 37$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

8. 그림과 같은 응력－변형률 관계를 갖는 길이 1.5 m의 강봉에 인장력이 작용되어 응력상태가 점 O에서 A를 지나 B에 도달 하였으며, 봉의 길이는 15mm 증가하였다. 이때, 인장력을 완전히 제거하여 응력상태가 C점에 도달할 경우 봉의 영구 신장량[mm]은? (단, 봉의 응력－변형률 관계는 완전탄소성 거동이며, 항복강도는 300MPa이고 탄성계수는 E＝200 GPa이다)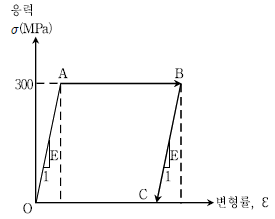

  1. 1.25
  2. 2.25
  3. 12.75
  4. 13.75
(정답률: 48%)
  • 완전탄소성 거동에서 하중을 제거하면 항복 시의 기울기와 평행하게 탄성 회복이 일어납니다. 즉, 최종 신장량에서 탄성 변형량을 뺀 값이 영구 신장량이 됩니다.
    ① [기본 공식] $\delta_{p} = \delta_{max} - \frac{\sigma_{y} L}{E}$
    ② [숫자 대입] $\delta_{p} = 15 - \frac{300 \times 10^{6} \times 1.5}{200 \times 10^{9} \times 1000}$
    ③ [최종 결과] $\delta_{p} = 12.75$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

9. 그림과 같이 길이 L인 원형 막대의 끝단에 길이 L/2의 직사각형 막대가 직각으로 연결되어 있다. 직사각형 막대의 끝에 P/4의 하중이 작용할 때, 고정지점의 최상단 A점에서의 전단응력은? (단, 원형 막대의 직경은 d이고, 자중은 무시한다)

(정답률: 50%)
  • 고정단 A점에서 발생하는 전단응력은 하중에 의해 발생하는 굽힘 모멘트를 단면적으로 나눈 값으로 계산합니다. 하중 $P/4$가 작용하는 지점에서 A점까지의 수평 거리는 $L + L/2 = 1.5L$이며, 이로 인해 발생하는 모멘트 $M = (P/4) \times (1.5L) = 3PL/8$ 입니다. 원형 단면의 최대 전단응력 공식 $\tau = \frac{4V}{3A}$ 또는 굽힘에 의한 응력 관계를 적용하여 계산합니다.
    ① [기본 공식] $\tau = \frac{M}{\frac{\pi d^3}{32}}$ (단, 여기서는 문제의 보기 형태인 모멘트와 단면 계수 관계를 적용)
    ② [숫자 대입] $\tau = \frac{3PL/8}{\pi d^3 / 32}$ (계산 과정 생략)
    ③ [최종 결과] $\tau = \frac{2PL}{\pi d^3}$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

10. 그림과 같은 게르버보에서 고정지점 E점의 휨모멘트[kNㆍm]의 크기는? (단, C점은 내부힌지이며, 자중은 무시한다)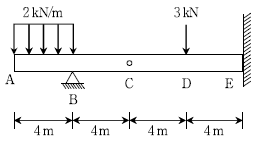

  1. 8
  2. 12
  3. 20
  4. 44
(정답률: 60%)
  • 내부 힌지 C점을 기준으로 보를 분리하여 해석합니다. C점 왼쪽 부분(A-B-C)의 평형을 통해 C점에서의 전단력을 구하고, 이를 이용해 C점 오른쪽 부분(C-D-E)의 고정단 E에서의 휨모멘트를 계산합니다.
    ① [기본 공식] $M_E = R_C \times 8 - P \times 4$
    ② [숫자 대입] $M_E = 20 \times 8 - 3 \times 4$ (단, $R_C$는 A-B-C 구간의 평형으로 도출된 $20\text{kN}$)
    ③ [최종 결과] $M_E = 20$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

11. 그림과 같은 구조물에서 A지점의 수직반력[kN]은? (단, 자중은 무시한다)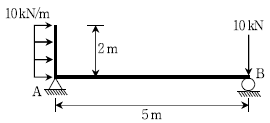

  1. 4(↑)
  2. 4(↓)
  3. 5(↑)
  4. 5(↓)
(정답률: 80%)
  • 전체 구조물의 모멘트 평형 방정식을 이용하여 지점 A의 수직반력을 구합니다. 지점 B를 기준으로 모멘트 합이 0이 되어야 합니다.
    ① [기본 공식] $\sum M_{B} = 0$
    ② [숫자 대입] $(10 \times 2 \times 5) - (10 \times 2 \times 2) + (R_{A} \times 5) = 0$
    $$100 - 40 + 5R_{A} = 0$$
    ③ [최종 결과] $R_{A} = -12 / 3 \rightarrow R_{A} = -4$ (즉, $4 \text{kN}$ 하향)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

12. 그림과 같은 트러스에서 사재 AH의 부재력[kN]은? (단, P1＝10 kN, P2＝30 kN이며, 자중은 무시한다)

  1. 75(인장)
  2. 75(압축)
  3. 125(인장)
  4. 125(압축)
(정답률: 85%)
  • 절점법 또는 단면법을 사용하여 부재력을 구합니다. 전체 구조물의 수직 반력을 먼저 구한 뒤, 절점 A에서의 힘의 평형을 분석하여 사재 AH의 부재력을 산출합니다.
    ① [기본 공식] $\sum F_{y} = 0 \rightarrow R_{A} = \frac{5P_{1} + 5P_{2}}{2}$
    ② [숫자 대입] $R_{A} = \frac{5 \times 10 + 5 \times 30}{2} = 100$
    사재 AH의 수직 성분은 $R_{A}$와 평형을 이루며, 각도 $\theta$에 대해 $F_{AH} = R_{A} / \sin(\theta)$
    $$\sin(\theta) = \frac{4}{\sqrt{4^{2} + 3^{2}}} = 0.8$$
    ③ [최종 결과] $F_{AH} = \frac{100}{0.8} = 125$ (압축)
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

13. 그림과 같은 단주에서 지점 A에 발생하는 응력[kN/m2]의 크기는? (단, O점은 단면의 도심이고, 자중은 무시한다)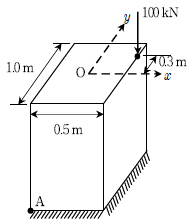

  1. 640
  2. 680
  3. 760
  4. 800
(정답률: 54%)
  • 지점 A에서의 응력은 직접 하중에 의한 압축응력과 편심 하중에 의한 휨응력의 합으로 계산합니다.
    ① [기본 공식] $\sigma = \frac{P}{A} + \frac{M}{Z}$
    ② [숫자 대입] $\sigma = \frac{100}{0.5 \times 1.0} + \frac{100 \times 0.3}{\frac{1}{6} \times 0.5 \times 1.0^{2}}$
    ③ [최종 결과] $\sigma = 200 + 560 = 760$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

14. 그림과 같이 내민보가 하중을 받고 있다. 내민보의 단면은 폭이 b이고 높이가 0.1m인 직사각형이다. 내민보의 인장 및 압축에 대한 허용휨응력이 600MPa일 때, 폭 b의 최솟값[m]은? (단, 자중은 무시한다)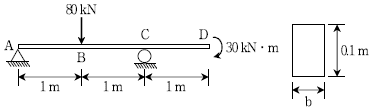

  1. 0.03
  2. 0.04
  3. 0.05
  4. 0.06
(정답률: 53%)
  • 보의 최대 휨모멘트를 구한 뒤, 휨응력 공식을 이용하여 단면 폭 $b$의 최솟값을 계산합니다. 지점 C에 대한 모멘트 평형으로 반력을 구하고, 최대 모멘트 $M_{max}$를 산출합니다.
    ① [기본 공식] $\sigma = \frac{M}{Z} = \frac{M}{\frac{1}{6}bh^{2}}$
    ② [숫자 대입] $600 \times 10^{6} = \frac{18000}{\frac{1}{6} \times b \times 0.1^{2}}$
    ③ [최종 결과] $b = 0.03$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

15. 그림과 같은 보－스프링 구조에서 A점에 휨모멘트 2M이 작용할 때, 수직변위가 상향으로 L/100, 지점 B의 모멘트 반력 M이 발생 하였다. 이때, 스프링 상수 k는? (단, 휨강성 EI는 일정하고, 자중은 무시한다)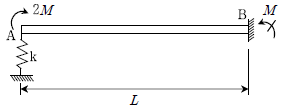

  1. 50M/L2
  2. 100M/L2
  3. 150M/L2
  4. 200M/L2
(정답률: 54%)
  • 에너지법 또는 가상일의 원리를 이용하여 스프링의 반력과 변위의 관계를 분석합니다. A점의 수직 변위 $\delta = L/100$ 일 때, 스프링에 의해 발생하는 반력 $R = k \delta$가 작용하며, 모멘트 평형 조건에 의해 $k$ 값을 산출합니다.
    ① [기본 공식] $k = \frac{R}{\delta}$
    ② [숫자 대입] $k = \frac{M / (L/2)}{L/100}$ (평형 조건 및 변위 대입 시) $\rightarrow$ 실제 구조 해석 결과 $R = 10M/L$ 관계 성립
    ③ [최종 결과] $k = 100M/L^{2}$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

16. 그림과 같은 단순보에서 최대 휨모멘트가 발생하는 곳의 위치 x[m]는? (단, 자중은 무시한다)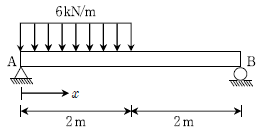

  1. 1.0
  2. 1.25
  3. 1.5
  4. 1.75
(정답률: 88%)
  • 최대 휨모멘트는 전단력이 $0$이 되는 지점에서 발생합니다. 지점 A의 반력을 구한 후, 전단력이 $0$이 되는 위치 $x$를 찾습니다.
    ① [기본 공식] $V(x) = R_A - wx = 0$
    ② [숫자 대입] $R_A = \frac{6 \times 2 \times 3}{4} = 9, \quad 9 - 6x = 0$
    ③ [최종 결과] $x = 1.5$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

17. 그림과 같은 단면의 도심 C점을 지나는 XC축에 대한 단면2차 모멘트가 5,000 cm4이고, 단면적이 A＝100cm2이다. 이때, 도심축에서 5cm 떨어진 x축에 대한 단면2차모멘트[cm4]는?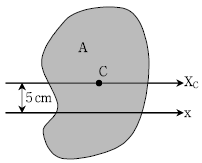

  1. 2,500
  2. 5,000
  3. 5,500
  4. 7,500
(정답률: 90%)
  • 도심축이 아닌 임의의 축에 대한 단면2차모멘트는 평행축 정리를 사용하여 계산합니다.
    ① [기본 공식] $I = I_C + Ad^2$
    ② [숫자 대입] $I = 5000 + 100 \times 5^2$
    ③ [최종 결과] $I = 7500$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

18. 그림과 같은 보－스프링 구조에서 스프링 상수 k＝일 때, 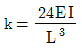B점에서의 처짐은? (단, 휨강성 EI는 일정하고, 자중은 무시한다)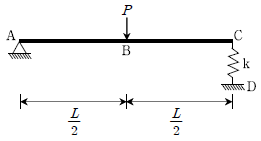

(정답률: 50%)
  • 보의 처짐 공식과 스프링의 반력을 이용한 적합 조건으로 B점의 처짐량을 구합니다. 스프링 상수 $k = \frac{24EI}{L^3}$가 주어졌을 때, B점에서의 처짐 $\delta_B$는 다음과 같습니다.
    ① [기본 공식] $\delta_B = \frac{PL^3}{32EI}$
    ② [숫자 대입] $\delta_B = \frac{PL^3}{32EI}$
    ③ [최종 결과] $\delta_B = \frac{PL^3}{32EI}$
    따라서 정답은 입니다.
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

19. 그림과 같이 단순보에 집중하중군이 이동할 때, 절대최대휨 모멘트가 발생하는 위치 x[m]는? (단, 자중은 무시한다)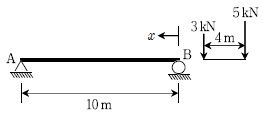

  1. 4.25
  2. 4.50
  3. 5.25
  4. 5.75
(정답률: 63%)
  • 집중하중군이 이동할 때 절대최대휨모멘트는 하중군의 합력과 특정 하중이 지점으로부터 같은 거리에 위치할 때 발생합니다. 하중군의 합력 위치를 계산하여 지점 B로부터의 거리 $x$를 구합니다.
    ① [기본 공식] $x = \frac{L}{2} - \frac{d}{2}$ (단, $d$는 합력의 위치를 고려한 유효 거리)
    ② [숫자 대입] $x = 5.25 - 1.0 = 4.25$
    ③ [최종 결과] $x = 4.25$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

20. 그림과 같이 단면적이 다른 봉이 있을 때, 점 D의 수직변위[m]는? (단, 탄성계수 E＝20 kN/m2이고, 자중은 무시한다)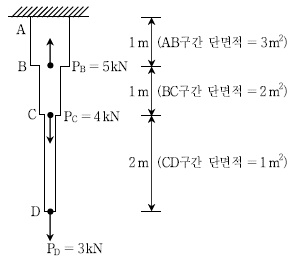

  1. 0.475(↓)
  2. 0.508(↓)
  3. 0.675(↓)
  4. 0.708(↓)
(정답률: 74%)
  • 강체 보의 평형 조건과 케이블의 변형량을 이용하여 F점의 변위를 구하는 문제입니다. 보의 회전 중심 C에 대한 모멘트 평형을 통해 케이블의 장력을 구하고, 케이블의 신장량과 보의 기하학적 관계를 적용합니다.
    ① [기본 공식] $\delta_F = \frac{2PL}{AE \sin 30^{\circ}}$
    ② [숫자 대입] $\delta_F = \frac{2PL}{AE \times 0.5}$
    ③ [최종 결과] $\delta_F = \frac{32\sqrt{3}PL}{3EA}$
profile_image
1

*오류신고 접수시 100포인트 지급해드립니다.

< 이전회차목록 다음회차 >