1과목: 과목 구분 없음
1. 그림과 같은 단순보에서 다음 항목 중 0의 값을 갖지 않는 것은? (단, 단면은 균일한 직사각형이다)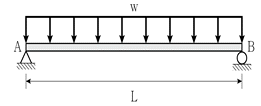
- 중립축에서의 휨응력(수직응력)
- 단면의 상단과 하단에서의 전단응력
- 양단지점에서의 휨응력(수직응력)
- 양단지점의 중립축에서의 전단응력
2. 그림과 같은 단순보에서 다음 설명 중 옳은 것은? (단, 단면은 균일한 직사각형이고, 재료는 균질하다)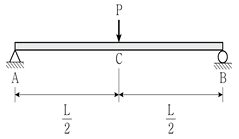
- 탄성계수 값이 증가하면 지점 처짐각의 크기는 증가한다.
- 지점 간 거리가 증가하면 지점 처짐각의 크기는 증가한다.
- 휨강성이 증가하면 C점의 처짐량은 증가한다.
- 지점 간 거리가 증가하면 C점의 처짐량은 감소한다.
3. 그림과 같은 게르버보에 하중이 작용하고 있다. A점의 수직반력 RA가 B점의 수직반력 RB의 2배(RA=2RB)가 되려면, 등분포 하중 w[kN/m]의 크기는? (단, 보의 자중은 무시한다)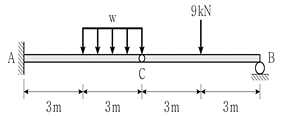
- 0.5
- 1.0
- 1.5
- 2.0
4. 그림과 같이 등분포 고정하중이 작용하는 단순보에서 이동하중이 작용할 때 절대 최대 전단력의 크기[kN]는? (단, 보의 자중은 무시한다)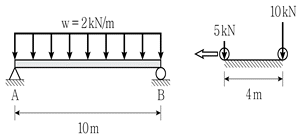
- 20
- 21
- 22
- 23
5. 그림과 같이 폭이 b이고 높이가 h인 직사각형 단면의 x축에 대한 단면2차모멘트 Ix1과 빗금친 직사각형 단면의 x축에 대한 단면2차모멘트 Ix2의 크기의 비 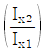 는?
는?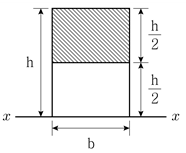
- 1/2
- 2/3
- 7/8
- 1
6. 그림과 같이 하중을 받는 구조물에서 고정단 C점의 모멘트 반력의 크기[kNㆍm]는? (단, 구조물의 자중은 무시하고, 휨강성 EI는 일정, MB=84kNㆍm이다)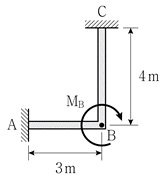
- 9
- 18
- 27
- 36
7. 그림과 같이 두 개의 우력모멘트를 받는 단순보 AE에서 A 지점 처짐각의 크기( 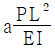 )와 C점 처짐의 크기(
)와 C점 처짐의 크기( 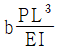 )를 구하였다. 상수 a와 b의 값은? (단, 보 AE의 휨강성 EI는 일정하고, 보의 자중은 무시한다)(순서대로 a, b)
)를 구하였다. 상수 a와 b의 값은? (단, 보 AE의 휨강성 EI는 일정하고, 보의 자중은 무시한다)(순서대로 a, b)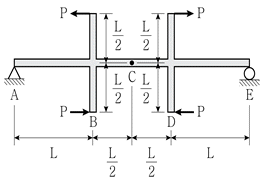
- 1/2, 5/8
- 1/2, 3/2
- 1/6, 5/8
- 1/6, 3/2
8. 그림과 같은 하중을 받는 단순보에서 인장응력이 발생하지 않기 위한 단면 높이 h의 최솟값[mm]은? (단, h=2b, 50kN의 작용점은 단면의 도심이고, 보의 자중은 무시한다)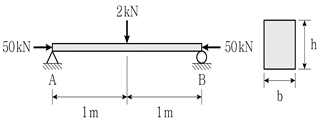
- 100
- 110
- 120
- 130
9. 그림과 같은 단순보의 C점에 스프링을 설치하였더니 스프링에서의 수직 반력이 P/2가 되었다. 스프링 강성 k는? (단, 보의 휨강성 EI는 일정하고 보의 자중은 무시한다)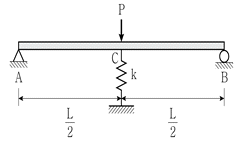
10. 보의 탄성처짐을 해석하는 방법에 대한 다음 설명으로 옳지 않은 것은?
- 휨강성 EI가 일정할 때, 모멘트 방정식
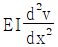 =M(x)를 두 번 적분하여 처짐 v를 구할 수 있는데, 이러한 해석법을 이중적분법(Double Integration Method)이라고 한다.
=M(x)를 두 번 적분하여 처짐 v를 구할 수 있는데, 이러한 해석법을 이중적분법(Double Integration Method)이라고 한다. - 모멘트면적정리(Moment Area Theorem)에 의하면, 탄성 곡선상의 점 A에서의 접선과 점 B로부터 그은 접선 사이의 점 A에서의 수직편차 tB/A는 M/EI선도에서 이 두 점 사이의 면적과 같다.
- 공액보를 그린 후 M/EI 선도를 하중으로 재하하였을 때, 처짐을 결정하고자 하는 곳에서 공액보의 단면을 자르고 그 단면에서 작용하는 휨모멘트를 구하여 처짐을 구할 수 있으며, 이러한 해석법을 공액보법(Conjugated Beam Method)이라고 한다.
- 카스틸리아노의 정리(Castigliano's Theorem)에 의하면, 한 점에 처짐의 방향으로 작용하는 어느 힘에 관한 변형 에너지의 1차 편미분 함수는 그 점에서의 처짐과 같다.
11. 그림과 같이 단순보에 2개의 집중하중이 작용하고 있을 때 휨모멘트선도는 아래와 같다. C점에 작용하는 집중하중 PC와 D점에 작용하는 집중하중 PD의 비(Pc/PD)는?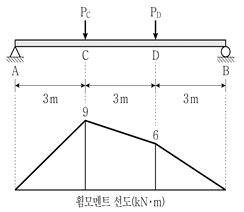
- 4
- 5
- 6
- 7
12. 그림과 같이 부재에 하중이 작용할 때, B점에서의 휨모멘트 크기[kNㆍm]는? (단, 구조물의 자중 및 부재의 두께는 무시한다)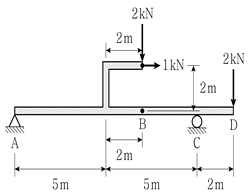
- 1
- 2
- 3
- 4
13. 그림과 같이 2개의 부재로 연결된 트러스에서 B점에 30kN의 하중이 연직방향으로 작용하고 있을 때, AB 부재와 BC 부재에 발생하는 부재력의 크기 FAB[kN]와 FBC[kN]는?(순서대로 FAB, FBC)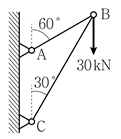
- 30, 30√3
- 30, 30
- 60, 60√3
- 60, 60
14. 그림과 같은 내민보에 집중하중이 작용하고 있다. 한 변의 길이가 b인 정사각형 단면을 갖는다면 B점에 발생하는 최대 휨응력의 크기는 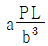 이다. a의 값은? (단, 보의 자중은 무시한다)
이다. a의 값은? (단, 보의 자중은 무시한다)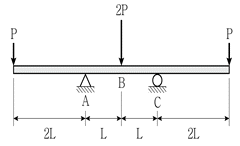
- 2
- 4
- 6
- 8
15. 그림과 같이 우력모멘트를 받는 단순보의 A 지점 처짐각의 크기는 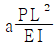 이다. a의 크기는? (단, 보의 휨강성 EI는 일정하고 보의 자중은 무시한다)
이다. a의 크기는? (단, 보의 휨강성 EI는 일정하고 보의 자중은 무시한다)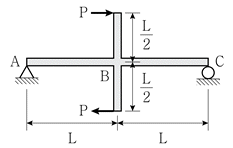
- 1/2
- 1/6
- 1/8
- 1/12
16. 그림과 같이 하중을 받는 스프링과 힌지로 지지된 강체 구조물에서 A점의 변위[mm]는? (단, MB=30Nㆍm, k1=k2=k3=5kN/m, L1=2m, L2=L3=1m, 구조물의 자중은 무시하며 미소변위이론을 사용한다)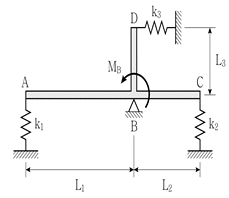
- 1.0
- 1.5
- 2.0
- 2.5
17. 그림과 같은 직사각형 단면(폭 b, 높이 h)을 갖는 단순보가 있다. 이 보의 최대휨응력이 최대전단응력의 2배라면 보의 길이(L)와 단면 높이(h)의 비(L/h)는? (단, 보의 자중은 무시한다)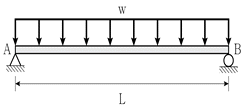
- 1/4
- 1/2
- 2
- 4
18. 그림과 같은 가새골조(Braced Frame)가 있다. 기둥 AB와 기둥 CD의 유효좌굴길이계수에 대한 설명으로 옳은 것은?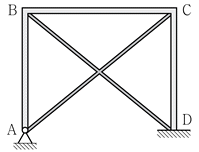
- 기둥 AB의 유효좌굴길이계수는 0.7보다 크고 1.0보다 작다.
- 기둥 AB의 유효좌굴길이계수는 2.0보다 크다.
- 기둥 CD의 유효좌굴길이계수는 0.5보다 작다.
- 기둥 CD의 유효좌굴길이계수는 1.0보다 크고 2.0보다 작다.
19. 그림 (a)와 같은 이중선형 응력변형률 곡선을 갖는 그림 (b)와 같은 길이 2m의 강봉이 있다. 하중 20kN이 작용할 때 강봉의 늘어난 길이[mm]는? (단, 강봉의 단면적은 200mm2이고, 자중은 무시하며, 그림 (a)에서 탄성계수 E1=100GPa, E2=40GPa이다)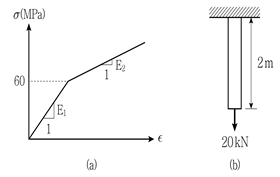
- 0.2
- 0.8
- 1.6
- 3.2
20. 다음 설명에서 틀린 것만을 모두 고르면?
- ㄱ, ㄷ
- ㄴ, ㄹ
- ㄱ, ㄴ, ㄹ
- ㄱ, ㄷ, ㄹ






이유는 단면의 중립축에서는 휨응력이 0이므로, 전단응력만이 존재합니다. 따라서 양단지점에서의 전단응력은 중립축에서의 전단응력과 같습니다.